HW 4

Question 1

Consider two investment opportunities. The first is a large water well project with a potential payoff of $100. The second opportunity is an investment series of 10 small wells, each with a potential payoff of $10. The probability that any well (large or small) returns a payoff is 0.1.

The functions below simulate the outcomes from the two investments.

big_well <- function(N) 100*rbinom(N, 1, 0.1)
sma_well <- function(N)  10*rbinom(N, 10, 0.1)

Write code that generates the long-run proportions for the small well investment opportunity.

Solution

set.seed(23586293)
d1 <- sma_well(100000)
table(d1) |> proportions()
d1
      0      10      20      30      40      50      60 
0.34697 0.38654 0.19672 0.05680 0.01127 0.00158 0.00012

Question 2

Create a figure which visualizes the long-run proportions.

Solution

t1 <- table(d1) |> proportions()
barplot(t1, ylim = c(0,max(t1)*1.1), xlab = "Investment outcome", ylab = "Propability")
box()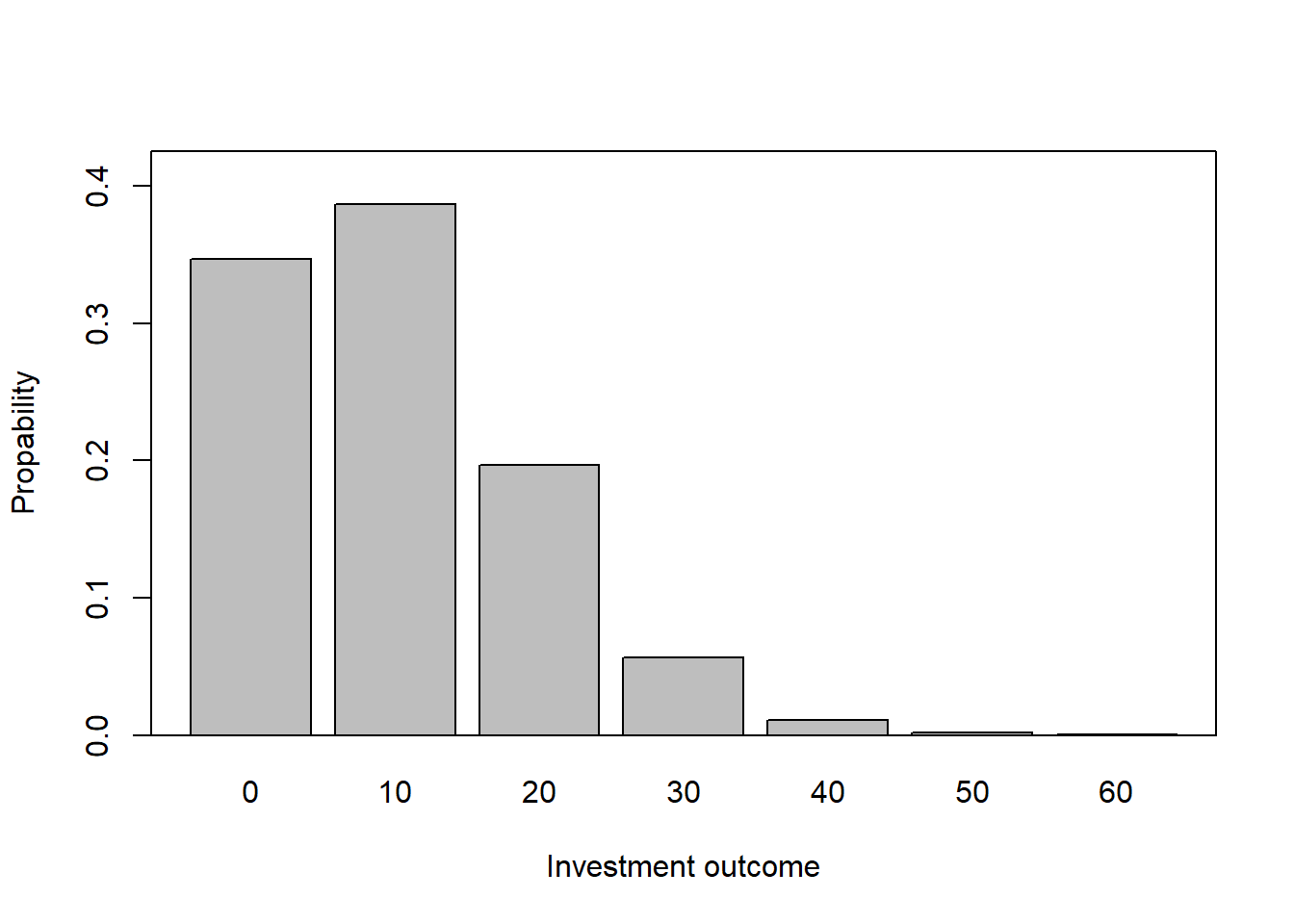

Question 3

Please read chapter 3 of Understanding Uncertainty. In section 3.9, the author introduces the notation p(E|K). What does K represent? Create an example where the probability of an event is different when K is different.

Question 4

If E denotes an event, what does Ec denote?

Question 5

Consider a potentially unfair six-sided die. Let E denote the outcome of a die roll. If P(E is even ) = .6, what must P(E is odd ) be? Why?

Question 6

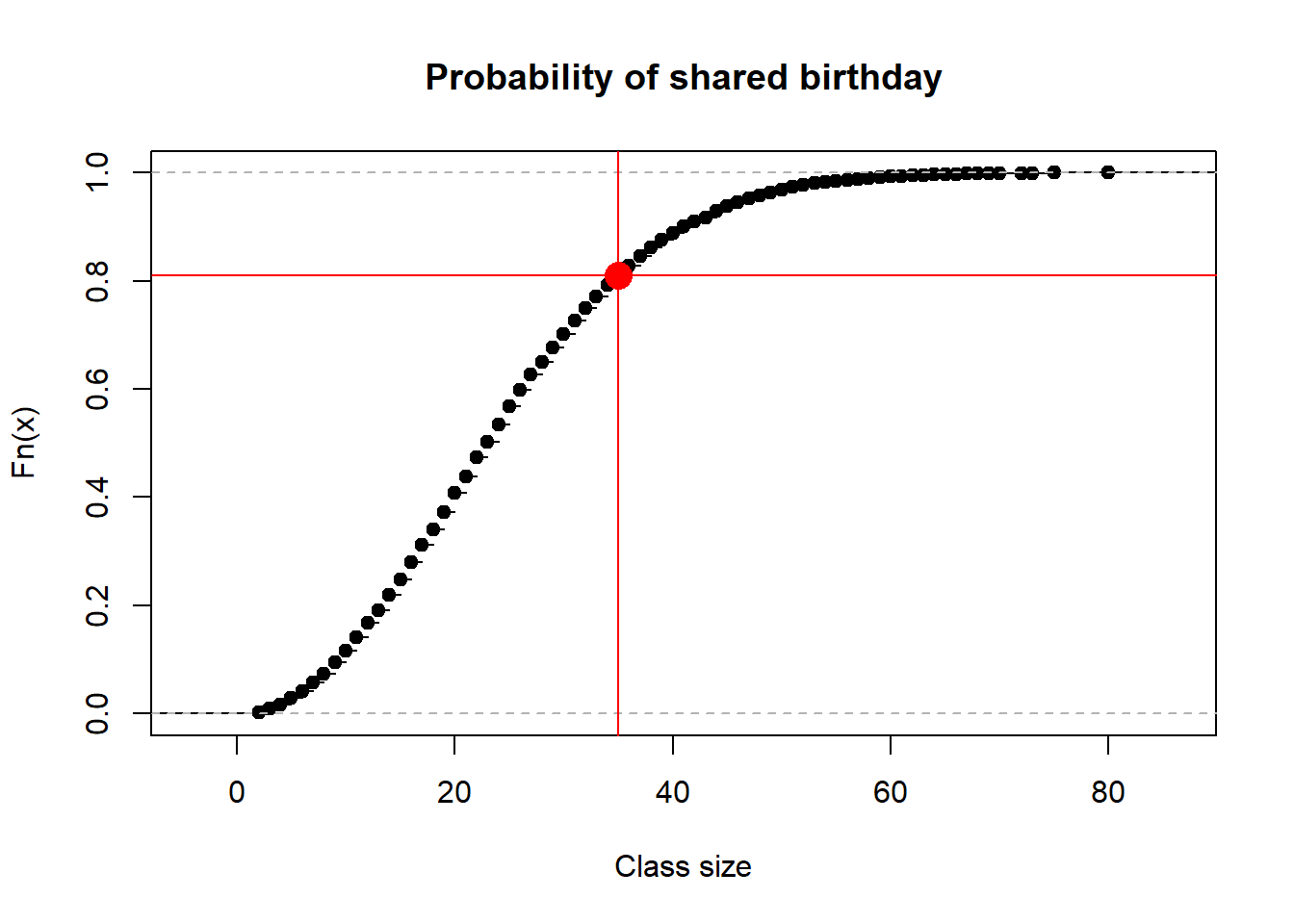
Using simulation, create a script that will solve the Birthday Problem: In a class of 35 individuals, what is the probability that at least two individuals will share a birthday? (The code we developed in class is below).

  1. What does set.seed do in the script?
  2. What does R represent?
  3. Does the solution make any assumptions or simplifications? If so, what are they?
  4. Run both versions of the script. For version 1, use a class size of 35. Do both versions give the same answer?
  5. Add vertical and horizontal lines to the plot generated in version 2 which show your estimated probability generated with version 1 code.
  6. Look at the first_duplicate function. What does the function return? Use ?which and ?min to read the documentation of what these commands do. (Answer: It returns the first instance of _____.)

Version 1 of code

generate_class <- function(class_size){
  sample(1:365, class_size, replace = TRUE)
}

check_birthday <- function(class){
  class |> duplicated() |> any()
}

set.seed(230583)
R <- 10000
replicates <- replicate(R, generate_class(35) |> check_birthday())
mean(replicates)
[1] 0.8106

Version 2 of code

first_duplicate <- function(){
    sample(1:365, 366, replace=TRUE) |>
    duplicated() |>
    which() |>
    min()
}

fd1 <- replicate(R, first_duplicate())
plot(ecdf(fd1), main = "Probability of shared birthday", xlab = "Class size")

abline(h=mean(replicates), col = "red")
abline(v=35, col = "red")
points(35, mean(replicates), pch = 16, cex = 2, col = "red")